My current research interests:
- Fundamental development for meshfree methods (reproducing kernel particle method (RKPM), peridynamics)
- Meshfree methods for finite-strain nonlinear solid mechanics
- Meshfree methods for geomechanics
- Meshfree methods for extreme event simulation
- Meshfree methods for convection dominated problems
- Meshfree methods for plates and shells
- Strong form collocation meshfree method
- Stabilized and variationally consistent formulations for meshfree and isogeometric analysis
- Accelerated numerical methods
- Modeling man-made and natural disasters (penetration/perforation, fragment-impact, blast-loaded structures, earthquake-induced landslides, slope stability analysis)
- Numerical methods for strong shock dynamics
- Unifying frameworks for particle methods
- Fluid-structure interaction using Lagrangian-Eularian schemes
- Immersed particle methods
- Continuum damage mechanics
- Computational fracture mechanics
- Discrete-continuum method coupling
- Multiscale methods based on energy-bridging and homogenization
- Method development and simulation of fracture and damage in concrete
- Method development and simulation of 3-D printing of concrete structures
- Method development and simulation of fused deposition modeling
- Topology optimization and adjoint methods
- Numerical methods for structural collapse
- Artificial intelligence
- Data mining
- Model order reduction
Computational formulations for natural and man-made disasters
|
Disasters, whether naturally occurring such as earthquakes, landslides, tsunamis, and storms, or man-made, e.g. those resulting from terrorism, contribute to a significant loss of life and property nationally and globally. Death tolls from one single natural disaster can range in the hundreds of thousands; cumulative tolls for man-made disasters (such as those during the war on terror) can be on the same magnitude. Effective numerical methods facilitate the advancement of protection against these disasters. My primary research focus is the development of robust and efficient numerical methods for extremely large deformation problems such as blast, fragment-impact processes and systems and components undergoing extreme conditions.
|
|
Perforation of a concrete block using a stabilized meshfree method
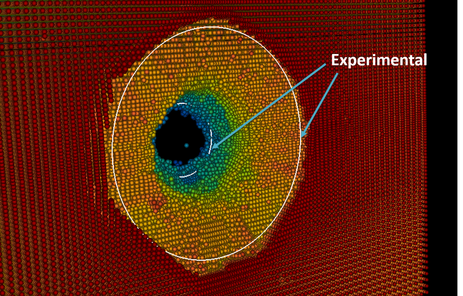
Numerical and experimental crater and hole
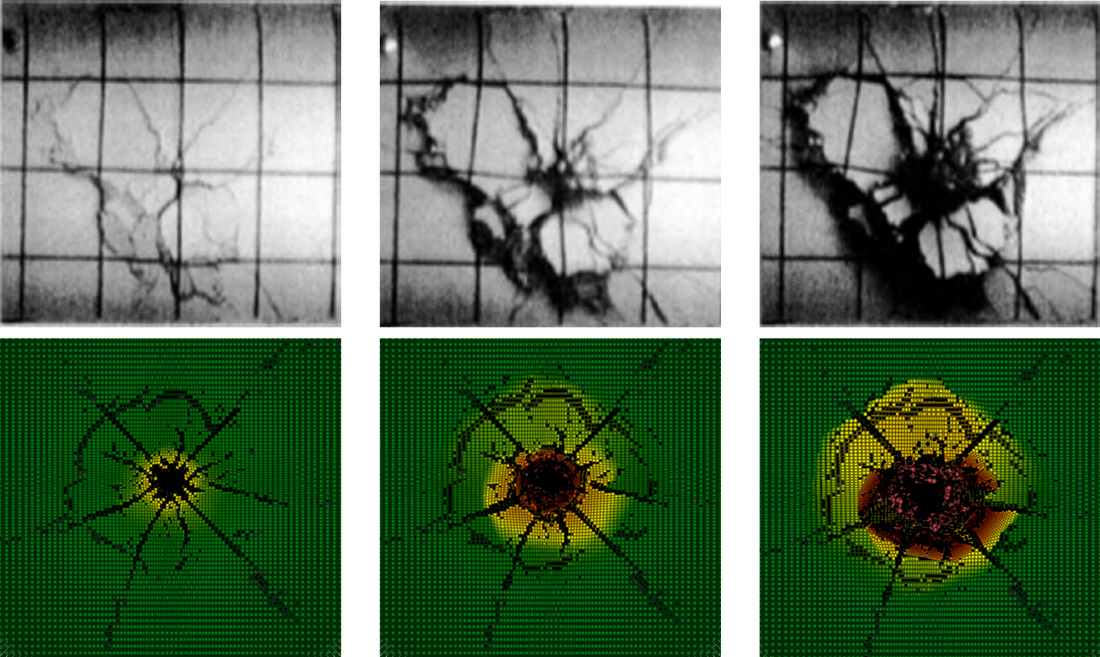
qualitative comparison of fragmentation in penetration event
|
I have developed a computational formulation called variationally consistent integration [1,2] to achieve high accuracy with low order domain integration for meshfree methods such as the reproducing kernel particle method (RKPM) [3,4], which alleviates the efficiency bottleneck associated with quadrature. It enables accurate and efficient simulations of material damage processes and structural failure, earth moving, damage assessment of landslides, and structures subjected to man-made and natural disasters. This research has been implemented into large-scale computational codes used by the Army ERDC, and Sandia National Laboratories, to model bullet penetration into geomaterials (concrete, soil) to numerically investigate damage mechanisms in these events, and facilitate advancement in protective structures. Simulation results have been validated under blind test prediction for various sizes of targets, projectile sizes, and velocities (figures to the left). Slope stability analyses (figure below), as well as simulations of full scale earth moving for Caterpillar have also been performed using the stabilized RKPM method J.S. Chen and I have developed [2,5-7].
Triggering of landslide due to 1989 Loma Prieta Earthquake
Subsequently, I developed an accelerated meshfree method [6], that exhibits high accuracy, stability, and very low computational cost (20x faster than previous methods), with excellent performance in large deformation problems involving fragment-impact and penetration, blast-loaded structures, slope stability, and metal forming problems (figures below).
|
Perforation problem with and without stabilization (tensile damage)
Steel plate subject to blast loading from the UCSD extreme event simulator
Overview and technical summary (article)
A great technical summary of this work can be found in this IACM Expressions article.
A great technical summary of this work can be found in this IACM Expressions article.
| 2016_expressions.pdf | |
| File Size: | 28271 kb |
| File Type: | |
References
[1] Chen, J. S., Hillman, M., Ruter, M., An arbitrary order variationally consistent method for Galerkin meshfree methods, International Journal for Numerical Methods in Engineering, Vol. 95, pp. 387-418, 2013, doi:10.1002/nme.4512.
[2] Hillman, M., Chen, J. S., Stabilized and variationally consistent nodal integration for meshfree modeling of impact problems, Computational Particle Mechanics, Vol. 1, pp. 245-256, 2014, doi:10.1007/s40571-014-0024-5.
[3] Liu, W. K., Jun, S., Zhang, Y. F.. Reproducing kernel particle methods. International Journal for Numerical Methods in Fluids, Vol. 20, pp. 1081-1106, 1995, doi: 10.1002/fld.1650200824.
[4] Chen, J.S., Pan, C., Wu, C.T., Liu, W. K. Reproducing Kernel Particle Methods for large deformation analysis of non-linear structures. Computer Methods in Applied Mechanics and Engineering, Vol 139, pp. 195–227, 1996, doi:10.1016/S0045-7825(96)01083-3.
[5] Sherburn, J.A.,Roth M.J. , Chen, J.S., Hillman, M., Meshfree modeling of concrete slab perforation using a reproducing kernel particle impact and penetration formulation, Int. J. Impact Eng. 86 (2015) 96–110. doi:10.1016/j.ijimpeng.2015.07.009.
[6] Hillman, M., Chen, J. S., An accelerated, convergent and stable nodal integration in Galerkin meshfree methods for linear and nonlinear mechanics, 2015, International Journal for Numerical Methods in Engineering, doi:10.1002/nme.5183.
[1] Chen, J. S., Hillman, M., Ruter, M., An arbitrary order variationally consistent method for Galerkin meshfree methods, International Journal for Numerical Methods in Engineering, Vol. 95, pp. 387-418, 2013, doi:10.1002/nme.4512.
[2] Hillman, M., Chen, J. S., Stabilized and variationally consistent nodal integration for meshfree modeling of impact problems, Computational Particle Mechanics, Vol. 1, pp. 245-256, 2014, doi:10.1007/s40571-014-0024-5.
[3] Liu, W. K., Jun, S., Zhang, Y. F.. Reproducing kernel particle methods. International Journal for Numerical Methods in Fluids, Vol. 20, pp. 1081-1106, 1995, doi: 10.1002/fld.1650200824.
[4] Chen, J.S., Pan, C., Wu, C.T., Liu, W. K. Reproducing Kernel Particle Methods for large deformation analysis of non-linear structures. Computer Methods in Applied Mechanics and Engineering, Vol 139, pp. 195–227, 1996, doi:10.1016/S0045-7825(96)01083-3.
[5] Sherburn, J.A.,Roth M.J. , Chen, J.S., Hillman, M., Meshfree modeling of concrete slab perforation using a reproducing kernel particle impact and penetration formulation, Int. J. Impact Eng. 86 (2015) 96–110. doi:10.1016/j.ijimpeng.2015.07.009.
[6] Hillman, M., Chen, J. S., An accelerated, convergent and stable nodal integration in Galerkin meshfree methods for linear and nonlinear mechanics, 2015, International Journal for Numerical Methods in Engineering, doi:10.1002/nme.5183.